Ориентированные графы
Орграф - это граф, все ребра которого имеют направление. Такие направленные ребра называются дугами. На рисунках дуги изображаются стрелочками (см. рис. 11.6).
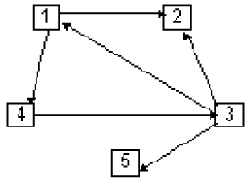
Рис. 11.6. Орграф
В отличие от ребер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги (дуга из нее исходит), вторая - концом дуги (дуга в нее входит). Можно сказать, что любое ребро - это пара дуг, направленных навстречу друг другу.
Если в графе присутствуют и ребра, и дуги, то его называют смешанным.
Все основные понятия, определенные для неориентированных графов (инцидентность, смежность, достижимость, длина пути и т.п.), остаются в силе и для орграфов - нужно лишь заменить слово "ребро" словом "дуга". А немногие исключения связаны с различиями между ребрами и дугами.
Степень вершины в орграфе - это не одно число, а пара чисел: первое характеризует количество исходящих из вершины дуг, а второе - количество входящих дуг.
Путь в орграфе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны, причем каждая вершина является одновременно концом одной дуги и началом следующей дуги. Например, в орграфе на рис. 11.6 нет пути, ведущего из вершины 2 в вершину 5. "Двигаться" по орграфу можно только в направлениях, заданных стрелками.
| Чайнворд | Слова | Совпадение последней и первой букв (возможность связать два слова в цепочку) |
| Стройка | Работы | Необходимое предшествование (например, стены нужно построить раньше, чем крышу, т. п.) |
| Обучение | Курсы | Необходимое предшествование (например, курс по языку Pascal полезно изучить прежде, чем курс по Delphi, и т.п.) |
| Одевание ребенка | Предметы гардероба | Необходимое предшествование (например, носки должны быть надеты раньше, чем ботинки, и т.п.) |
| Европейский город | Перекрестки | Узкие улицы с односторонним движением |
| Организация | Сотрудники | Иерархия (начальник - подчиненный) |